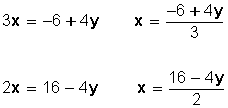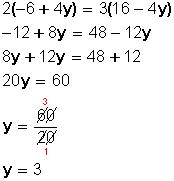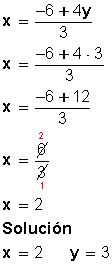Concepto de hipótesis
Es una proposición que establece relaciones, entre los hechos; para otros es una posible solución al problema; otros mas sustentan que la hipótesis no es mas otra cosa que una relación entre las variables, y por último, hay quienes afirman que es un método de comprobación.
Origen de la hipótesis
Selltiz (1974:53) señala:
"Una hipótesis puede estar basada simplemente en una sospecha, en los resultados de otros estudios y la esperanza de que una relación entre una o mas variables se den en el estudio en cuestión. O pueden estar basadas en un cuerpo de teorías que, por un proceso de deducción lógica, lleva a la predicción de que, si están presentes ciertas condiciones, se darán determinados resultados.
La elaboración de una buena hipótesis tiene como punto de partida el conocimiento del área en la que se desea hacer la investigación, sin este conocimiento previo se corre el riesgo de recorrer caminos ya transitados y trabajar en temas ya tratados que carecen de interés para la ciencia.
Si la hipótesis se basa u origina de otros estudios, la investigación estará en clara relación con un cuerpo de conocimientos ya existentes, probados, por lo que el trabajo será una contribución que permitirá reforzar ese cuerpo de conocimientos.
Función de la Hipótesis:
Cuando se describe su importancia, se plantean algunas de las funciones que ellas cumplen, porque además de ser guías en el proceso de investigación, también pueden servir para indicar que observaciones son pertinentes y cuales no lo son con respecto al problema planteado.
La hipótesis puede señalar loas relaciones o vínculos existentes entre las variables y cuales de ellas se deben estudiar, sugieren una explicación en ciertos hechos y orientan la investigación en otros, sirve para establecer la forma en que debe organizarse eficientemente el análisis de los datos. Hernández agrega que entre otras funciones, su objetivo principal, es de aprobar y sugerir teorías.
Formulación de Hipótesis:
Es un planteamiento que elabora el investigador a partir de la observación de una realidad que tiene explicación en una teoría, por lo tanto se afirma que ellas representan un punto medio entre la teoría y la realidad.
Clasificación de la hipótesis
Las hipótesis pueden adoptar diferentes valores y clasificarse de acuerdo a los criterios del investigador:
- Hipótesis general: es cuando trata de responder de forma amplia a las dudas que el investigador tiene acerca de la relación que existe entre las variables.
- Hipótesis específica: es específica aquella hipótesis que se deriva de la general, estas tratan de concretizar a la hipótesis general y hace explícitas las orientaciones concebidas para resolver la investigación.
- Hipótesis estadística: la hipótesis estadística es aquella hipótesis que somete a prueba y expresa a las hipótesis operacionales en forma de ecuaciones matemáticas.
- Problema: se quiere determinar si el entrenamiento en técnicas de estudio mejora el rendimiento académico de los estudiantes de la UNELLEZ.
- Hipótesis específica: los alumnos del subproyecto lenguaje y comunicación del I semestre, programa educación integral, entrenados en técnicas de estudio, obtendrán altas calificaciones al mejorar sus técnicas de aprendizajes.
- Hipótesis operacional: el promedio de rendimiento de los alumnos del subproyecto lenguaje y comunicación, sometidos a entrenamientos en técnicas de estudio (grupo experimental), será mayor que el promedio de rendimiento de aquellos alumnos no sometidos al entrenamiento (grupo control).
- Hipótesis estadística:
- Hipótesis nula: (X1) = (X2); no existe relación en los promedios obtenidos por los estudiantes entrenados en técnicas de estudio (X1) y los no entrenados (X2)
- Hipótesis alternativas: X1 > X2; los alumnos sometidos a entrenamientos en técnicas de elaboración de resumen (X1) obtuvieron mejor promedio de rendimiento que aquellos alumnos que no recibieron ningún tipo de entrenamiento (X2).
Requisitos para la elaboración de hipótesis:
La formulación de hipótesis es una tarea que se logra cuando se cumple con algunos requisitos, entre ellos:
- Formularse en términos claros, es decir, emplear palabras precisas que no den lugar a múltiples interpretaciones. La claridad con que se formulen es fundamental, debido a que constituyen una guía para la investigación.
- Tener un referente empírico, ello hace que pueda ser comprobable. Una hipótesis sin referente empírico se transforma en un juicio de valor al no poder ser comprobable, verificable, carece de validez para la ciencia.
Evaluación de la Hipótesis:
Existe algunos criterios que sirven de guía para determinar si la hipótesis cumple con algunos requisitos Mc Güigan (1971: 67) afirma:
- Permite ser comprobada, es decir, establece claramente su referente empírico.
- Está en correlación y armonía con el conjunto de las hipótesis del proyecto de la investigación
- Responde en términos claros y precisos al problema planteado, es decir, señala la relación que se espera de las variables.
- Son susceptibles de ser cuantificadas.
Dificultades en la Elaboración de la Hipótesis:
La hipótesis resulta una tarea ardua, de difícil elaboración, esta dificultad generalmente proviene de circunstancias tales como:
- Un planteamiento poco claro del problema a investigar
- Falta de conocimiento del marco teórico de la investigación como consecuencia de la poca claridad que se tiene del problema que se desea resolver.
- Carencia de habilidad para desarrollar y utilizar el referente teórico – conceptual.
- En general, por el desconocimiento de los procesos de la ciencia y la investigación, por lo tanto ausencia de criterios para la elaboración de hipótesis y selección de técnicas de investigación adecuadas al problema que se investiga.
Las características de una hipótesis
- Deben referirse a una situación social real; esto es que debe ser racional, y sobre todo que exista, sino estaríamos hablando de un mundo imaginario y de ensueño.
- Debe ser lógica y acorde con fenómenos conocidos y no estar en conflicto con leyes o principios ya establecidos: Se refiere al principio de economicidad de la ciencia, el cual nos dice que hay que retomar lo que ya esta aceptado para no tener que empezar desde cero, y a su vez aportar algo.
- La relación entre variables propuesta por una hipótesis debe ser clara y verosímil (lógica); Esto es que la hipótesis debe ser clara y creíble (Posteriormente veremos qué es una variable).
- Los términos (variables) de la hipótesis tienen que ser comprensibles: Esto es que tenga una adecuación entre la gente a la que será dirigida con el lenguaje utilizado en la proposición.
- Las hipótesis deben de ser la transformación directa de las preguntas de la investigación: es decir, que estas nos ayudan a saber que es lo que buscamos y como lo buscamos.
- Las hipótesis deben ser medibles: Este punto es uno de los más importantes, pues como ya se había dejado claro, las hipótesis deben ser comprobadas para poder llegar a un conocimiento, y la única forma de poder probarlas, es que tengan la capacidad de ser medibles.
- Las expresiones de hipótesis deben de ser libres de los valores propios del investigador: Esto habla más que nada de que no debe haber subjetividad ni manipulación de hipótesis por parte de quien la formula, sino por el contrario, que deben ser objetivas.
Concepto de variables
Variables:
La definición más sencilla, es la referida a la capacidad que tienen los objetos y las cosas de modificar su estado actual, es decir, de variar y asumir valores diferentes. Briones (1987: 34) define: "Una variable es una propiedad, característica o atributo que puede darse en ciertos sujetos o pueden darse en grados o modalidades diferentes. . . son conceptos clasificatorios que permiten ubicar a los individuos en categorías o clases y son susceptibles de identificación y medición".
Clasificación de las variables
Variable:
Variables Discretas; Variables Continuas; Variable Cuantitativa; Variables Cualitativas; Variable Interviniente; Variable Dependiente; Independiente.
Variable Dependiente
Variable dependiente es el factor que es observado y medido para determinar el efecto de la variable independiente.
Variable Interviniente
Aquellas características o propiedades que de una manera u otra afectan el resultado que se espera y están vinculadas con las variables independientes y dependientes.
Variable Moderadora
Tuckman: representan un tipo especial de variable independiente, que es secundaria, y se selecciona con la finalidad de determinar si afecta la relación entre la variable independiente primaria y las variables dependientes.
Variables Cualitativas
Aquellas que se refieren a atributos o cualidades de un fenómeno. Sabino (1989: 80) señala que sobre este tipo de variable no puede construirse una serie numérica definida.
Variable Cuantitativa
Aquellas variables en las que características o propiedades pueden presentarse en diversos grados de intensidad, es decir, admiten una escala numérica de medición.
Variables Continuas
Aquellas que pueden adoptar entre dos números puntos de referencias intermedio. Las calificaciones académicas (10.5, 14.6, 18.7, etc.)
Variables Discretas
Aquellas que no admiten posiciones intermedias entre dos números. Ej., en Barinas la división de territorial la constituyen 11 municipios por no (10.5 u 11.5 municipios).
Variables de Control
Tuckman: La define como esos factores que son controlados por el investigador para eliminar o neutralizar cualquier efecto que podrían tener de otra manera en el fenómeno observado
Operacionalización de la Variable
Es un paso importante en el desarrollo de la investigación. Cuando se identifican las variables, el próximo paso es su operacionalización.
Comprende tres tipos de definiciones:
- Nominal: es el nombre de la variable que le interesa al investigador.
- Real: consiste en determinar las dimensiones que contienen las variables nominales.
- Operacional: o indicadores. Esta da la base para su medición y la definición de los indicadores que constituyen los elementos más concretos de una variable y de donde el investigador derivará los ítems o preguntas para el instrumento con que recolectará la información.
Los indicadores
Entre los ámbitos más afectados por la globalización se encuentra la rendición de cuentas en la forma de ejercicio del gobierno, así como establecer nuevos requisitos y lineamientos para la elaboración de estadísticas e indicadores de los países. En este trabajo se exponen algunos de los efectos y requerimientos a que se enfrentan los generadores de estadísticas del país.
Introducción
Uno de los actuales retos de la generación de estadísticas del país es contar con información relevante y oportuna para la toma de decisiones y el seguimiento de los compromisos internacionales de México. Los indicadores estadísticos, sin duda, constituyen una de las herramientas indispensables para el logro de estas acciones y una de las tareas del INEGI es fomentar la cultura para su correcta construcción y aplicación. A continuación, se presenta una breve guía de lo que son los indicadores, sus características, utilidad, tipos y limitaciones para, finalmente, enmarcar la importancia que han adquirido y los retos que imponen a los generadores de estadísticas del país.
¿Qué es un indicador?
No existe una definición oficial por parte de algún organismo nacional o internacional, sólo algunas referencias que los describen como: "Herramientas para clarificar y definir, de forma más precisa, objetivos e impactos (...) son medidas verificables de cambio o resultado (...) diseñadas para contar con un estándar contra el cual evaluar, estimar o demostrar el progreso (...) con respecto a metas establecidas, facilitan el reparto de insumos, produciendo (...) productos y alcanzando objetivos". Una de las definiciones más utilizadas por diferentes organismos y autores es la que Bauer dio en 1966: "Los indicadores sociales (...) son estadísticas, serie estadística o cualquier forma de indicación que nos facilita estudiar dónde estamos y hacia dónde nos dirigimos con respecto a determinados objetivos y metas, así como evaluar programas específicos y determinarsu impacto". Si bien los indicadores pueden ser cualitativos o cuantitativos, en este trabajo nos abocaremos únicamente a los segundos.
Características de los indicadores
- Estar inscrito en un marco teórico o conceptual, que le permita asociarse firmemente con el evento al que el investigador pretende dar forma. De ser posible, debe establecerse una estructura que lo ubique en un marco explicativo, como es el caso del modelo presión-estado- respuesta (PER) que utiliza la Organización para la Cooperación y el Desarrollo Económico (OCDE) para el trabajo con indicadores de medio ambiente, que los organiza para referenciar situaciones de presión, de estado o de respuesta en torno al tema.
- Ser específicos, es decir, estar vinculados con los fenómenos económicos, sociales, culturales o de otra naturaleza sobre los que se pretende actuar; por lo anterior, se debe contar con objetivos y metas claros, para poder evaluar qué tan cerca o lejos nos encontramos de los mismos y proceder a la toma de decisiones pertinentes. Deben mostrarse especificando la meta u objetivo a que se vinculan y/o a la política a la que se pretende dar seguimiento; para cumplirlas se recomienda que los indicadores sean pocos.
- Ser explícitos, de tal forma que su nombre sea suficiente para entender si se trata de un valor absoluto o relativo, de una tasa, una razón, un índice, etc., así como a qué grupo de población, sector económico o producto se refieren y si la información es global o está desagregada por sexo, edad, años o región geográfica.
- Estar disponibles para varios años, con el fin de que se pueda observar el comportamiento del fenómeno a través del tiempo, así como para diferentes regiones y/o unidades administrativas. La comparabilidad es un insumo que permite fomentar el desarrollo social o económico de acuerdo con lo que tenemos respecto a los demás o a otros momentos;de hecho, nociones socioeconómicas como producción, pobreza y trabajo sólo son comprensibles en términos relativos.
- Deben ser relevantes y oportunos para la aplicación de políticas, describiendo la situación prevaleciente en los diferentes sectores de gobierno, permitiendo establecer metas y convertirlas en acciones.
- Los indicadores no son exclusivos de una acción específica; uno puede servir para estimar el impacto de dos o más hechos o políticas, o viceversa. Sólo de manera excepcional, un indicador proveerá información suficiente para la comprensión de fenómenos tan complejos como la educación o la salud; por lo que, para tener una evaluación completa de un sector o un sistema, se requiere de un conjunto de indicadores que mida el desempeño de las distintas dependencias y/o sectores y proporcione información acerca de la manera como éstos trabajan conjuntamente para producir un efecto global.
- Ser claro, de fácil comprensión para los miembros de la comunidad, de forma que no haya duda o confusión acerca de su significado, y debe ser aceptado, por lo general, como expresión del fenómeno a ser medido. Para cada indicador debe existir una definición, fórmula de cálculo y metadatos necesarios para su mejor entendimiento y socialización. Por lo anterior, es importante que el indicador sea confiable, exacto en cuanto a su metodología de cálculo y consistente, permitiendo expresar el mismo mensaje o producir la misma conclusión si la medición es llevada a cabo con diferentes herramientas, por distintas personas, en similares circunstancias.
- Que la recolección de la información permita construir el mismo indicador de la misma manera y bajo condiciones similares, año tras año, de modo que las comparaciones sean válidas.
- Técnicamente debe ser sólido, es decir, válido, confiable y comparable, así como factible, en términos de que su medición tenga un costo razonable.
- Ser sensible a cambios en el fenómeno, tanto para mejorar como para empeorar. Ejemplos de cómo un indicador puede desviarse de medir la efectividad de una política, se encuentran de manera frecuente en el tema de medio ambiente, como cuando se tuvo que descartar el desuperficie afectada por incendiospara medir la efectividad de las acciones de gobierno, debido a que su comportamiento también depende de factores naturales no controlables.
- Si bien su selección no debe depender de la disponibilidad de información proveniente de encuestas, censos y/o registros administrativos, sino de los objetivos fijados en los programas y proyectos de gobierno (dentro de los cuales se inscriben), es importante considerar el costo-beneficio del tiempo y los recursos necesarios para su construcción, por lo que, de preferencia, debe ser medibles a partir del acervo de datos disponible.
Utilidad
Los indicadores son elementales para evaluar, dar seguimiento y predecir tendencias de la situación de un país, un estado o una región en lo referente a su economía, sociedad, desarrollo humano, etc., así como para valorar el desempeño institucional encaminado a lograr las metas y objetivos fijados en cada uno de los ámbitos de acción de los programas de gobierno. La comparabilidad del desarrollo económico y social es otra de las funciones de los indicadores, ya que estamos inscritos en una cultura donde el valor asignado a los objetos, logros o situaciones sólo adquiere sentido respecto a la situación de otros contextos, personas y poblaciones, es decir, es el valor relativo de las cosas lo que les da un significado.
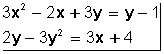
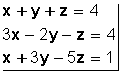
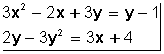
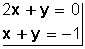es de primer grado con dos incógnitas (porque todos los valores están elevados a 1, que no se escribe).
.
